The Algorithms – Dart
所有用 Dart 实现的算法(用于教育)
这些实现仅用于学习目的。它们可能不如 Dart 标准库中的实现高效。
算法列表
请参阅我们的 目录 以获取所有算法的完整列表。此处将解释其中一些算法(最常见的)。
搜索算法
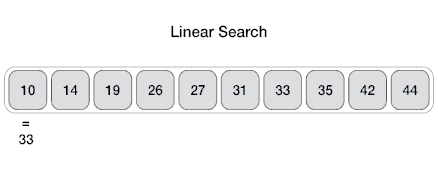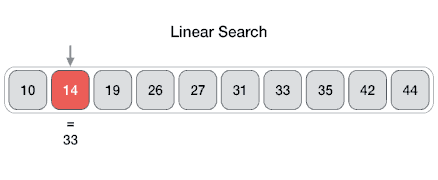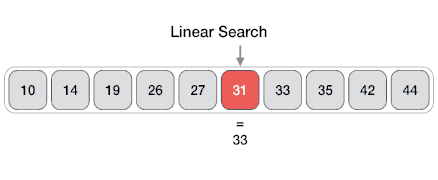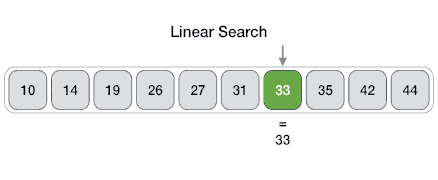
线性
来自 Wikipedia:线性搜索或顺序搜索是用于在列表中查找目标值的检索方法。它依次检查列表中的每个元素以查找目标值,直到找到匹配项或搜索完所有元素为止。线性搜索的最坏情况运行时间为线性时间,最多进行 n 次比较,其中 n 是列表的长度。
属性
- 最坏情况性能 O(n)
- 最佳情况性能 O(1)
- 平均情况性能 O(n)
- 最坏情况空间复杂度 O(1) 迭代
二分
来自 Wikipedia:二分搜索,也称为半区间搜索或对数搜索,是一种搜索算法,用于在已排序的数组中查找目标值的位置。它将目标值与数组的中间元素进行比较;如果它们不相等,则将目标值不可能存在的半部分排除,并在剩余的半部分中继续搜索,直到成功为止。
属性
- 最坏情况性能 O(log n)
- 最佳情况性能 O(1)
- 平均情况性能 O(log n)
- 最坏情况空间复杂度 O(1)
排序算法
气泡
来自 Wikipedia:冒泡排序,有时也称为沉降排序,是一种简单的排序算法,它重复地遍历要排序的列表,比较每对相邻的项,并在顺序错误时交换它们。列表遍历会重复进行,直到不需要交换为止,这表示列表已排序。
属性
- 最坏情况性能 O(n^2)
- 最佳情况性能 O(n)
- 平均情况性能 O(n^2)
观看 动作中的算法
插入
来自 Wikipedia:插入排序是一种简单的排序算法,它一次构建一个已排序的数组(或列表)。与快速排序、堆排序或归并排序等更高级的算法相比,它在处理大型列表时效率要低得多。
属性
- 最坏情况性能 O(n^2)
- 最佳情况性能 O(n)
- 平均情况性能 O(n^2)
观看 动作中的算法
快速
来自 Wikipedia:快速排序(有时称为划分交换排序)是一种有效的排序算法,它是一种系统地将数组元素进行排序的方法。
属性
- 最坏情况性能 O(n^2)
- 最佳情况性能 O(n log n) 或 O(n)(使用三向划分)
- 平均情况性能 O(n^2)
观看 动作中的算法
选择
来自 Wikipedia:该算法将输入列表分为两部分:已排序的项子列表,它从左到右在列表的前部(左侧)构建,以及未排序的项子列表,它们占据列表的其余部分。最初,已排序的子列表为空,未排序的子列表是整个输入列表。该算法通过在未排序的子列表中查找最小(或最大,取决于排序顺序)的元素,将其与最左侧的未排序元素交换(将它放到已排序状态),然后将子列表边界向右移动一个元素来执行。
属性
- 最坏情况性能 O(n^2)
- 最佳情况性能 O(n^2)
- 平均情况性能 O(n^2)
观看 动作中的算法
归并
来自 Wikipedia:归并排序(也通常拼写为 mergesort)是一种分而治之的算法,由 John von Neumann 于 1945 年发明。该算法首先将列表划分为最小单元(1 个元素),然后将每个元素与相邻列表进行比较以排序和合并两个相邻列表。最后,所有元素都已排序和合并。它是一种有效的、通用的、基于比较的排序算法。
属性
- 最坏情况性能 O(n log n)
- 最佳情况性能 O(n log n)
- 平均情况性能 O(n log n)
观看 动作中的算法
希尔
来自 Wikipedia:希尔排序是插入排序的泛化,它允许交换相距很远的项。其思想是排列元素列表,使得从任何位置开始,每隔 n 个元素都能得到一个排序列表。这样的列表称为 h 排序。等效地,可以将其视为 h 个交错的列表,每个列表都单独排序。
属性
- 最坏情况性能 O(n log^2 2n)
- 最佳情况性能 O(n log n)
- 平均情况性能取决于间隔序列
观看 动作中的算法
时间复杂度图
比较排序算法(冒泡排序、插入排序、选择排序)的复杂度
社区频道
我们已加入 Gitter!欢迎加入我们。
贡献
请阅读我们的 CONTRIBUTING.md。